Nits, Lux, Lumen, Candela - calculating with light and lighting

When the sun is at its zenith at midday in summer, that's around 90000 lux. The new lamp for the bathroom should be 400 lumens bright. A candle has a brightness of 1 candela, and the display of a notebook is described as 300 nits.

These are all specifications that have something to do with brightness, but each of these examples uses different units. How are they related? In fact, these are mostly official physical units and not misleading marketing - they just describe slightly different aspects of light and illumination. If we know which unit stands for which physical property, then the sky in summer can also be compared with the lamp and the display.

Radiant power

Let's start with radiant power. As with mechanical power, radiant power describes an amount of energy per unit of time. In the case of radiant power, this energy is transported in the form of electromagnetic waves. And just as with mechanical power, the unit of radiant power is the watt.

The term radiant power is used for all electromagnetic waves, not just visible light. The specification in (milli-)watts can also be found, for example, in wifi routers, which in practically all countries have an upper limit of radiated power that they are not allowed to exceed.

The only special thing about visible light is the fact that our eyes can perceive it (and this has developed evolutionary because our star has its highest radiant power in this wavelength range).

However, even in the visible light range, i.e. at wavelengths between approx. 400 nm and 780 nm, we humans do not see the radiation as is, but perceive it with varying degrees of accuracy depending on the wavelength. This is because we have different cones and rods in our retina for each of these wavelengths, which have different abilities at processing this radiation depending on the respective wavelength. Because we are mostly interested in what we can actually see and less in what is objectively emitted, physics distinguishes between radiometric properties, which describe the radiation itself, and photometric properties, which describe what we can perceive.

Luminous flux

In addition to the radiometric radiant power, a photometric counterpart was therefore introduced: the luminous flux.

The luminous flux describes the radiant power in relation to the sensitivity of the human eye. Because this sensitivity is wavelength-dependent, the sensitivity at 555 nm (the color green) was set as the reference for the definition because this wavelength corresponds to the most sensitive point on the brightness sensitivity curve.

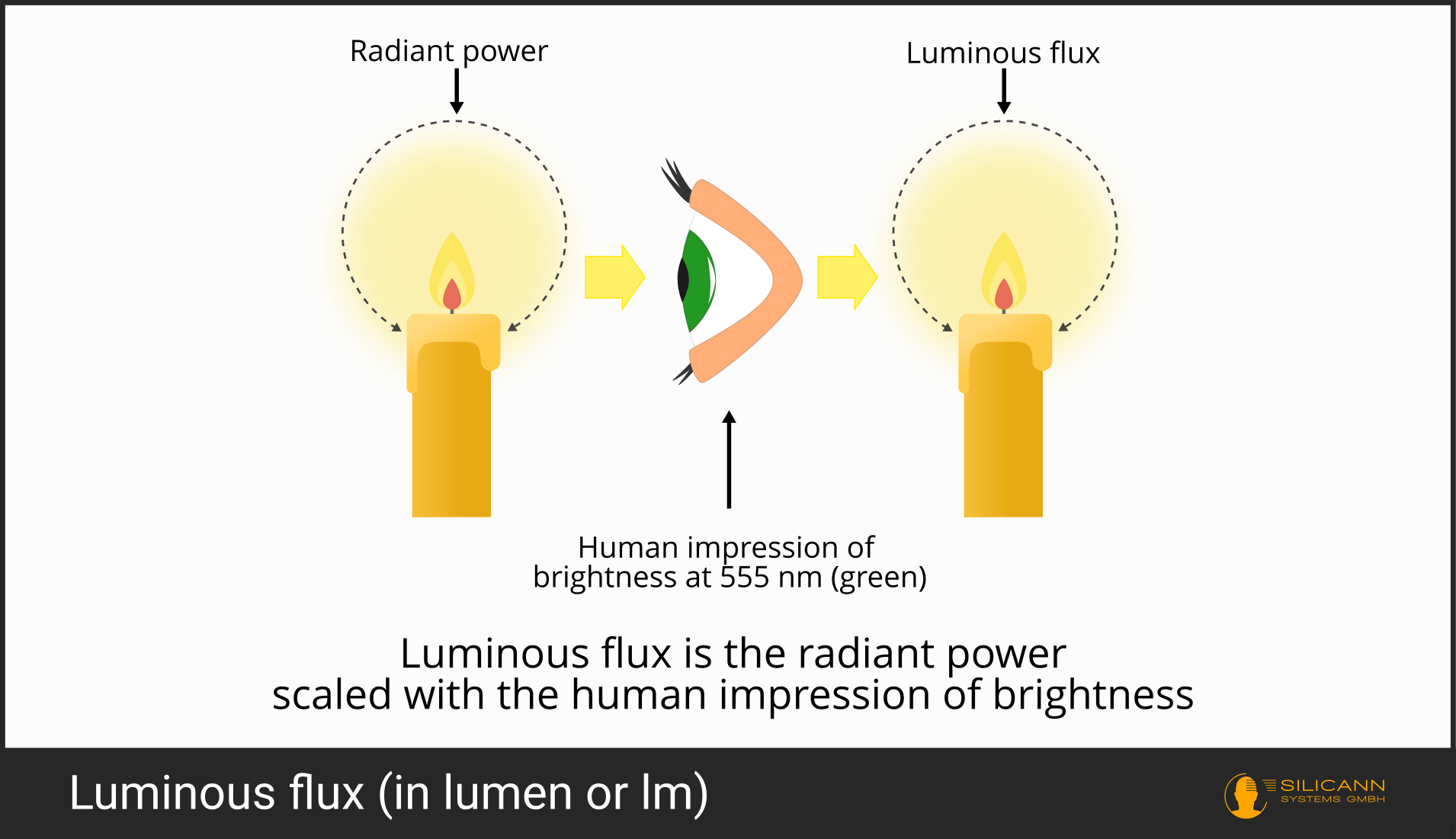
This photometric approach would not change the unit watt in purely mathematical terms: The sensitivity at each wavelength would only be a factor, a number without a unit, so that in the end the unit would again be the watt. However, to ensure that the unit clearly indicates whether it is the radiometric radiant power or the photometric luminous flux, a new unit has been introduced for the luminous flux: the lumen.

At a wavelength of 555 nm, the conversion ratio is 683 lm/W. As we perceive less at other wavelengths with the same radiant power, the scaling factor is lower in these cases.

If the value is not specified further, and this is usually the case in practice, then it is our perception of brightness for daytime vision. Daytime vision is determined by the cones in our retina, which we also use for color perception. The rods, on the other hand, are only used for night vision. Because we only have one form of them and not three as with the cones, we cannot distinguish the wavelengths with their help - which is why all cats appear so gray to us at night. However, the rods are much more sensitive: for night vision and the most sensitive wavelength, 507 nm, 1 watt of radiant power corresponds to a luminous flux of 1700 lm.

Luminous intensity

The luminous flux describes the total visible light emitted by the light source. Sometimes, however, we are only interested in the light within a certain solid angle, not the entire light. An example would be street lighting: the goal is an illuminated street, not the illuminated sky. We are therefore only interested in the part of the luminous flux that is emitted in the direction of the road. This ratio of luminous flux and solid angle is the luminous intensity.

Just as an angle describes the section of a circle, the solid angle is a section of a sphere. The unit of solid angle is called the steradian, abbreviated sr. If we consider a sphere with a radius of one meter, then a solid angle of 1 sr describes a section of a circle whose area is exactly 1 m². A full sphere would have a solid section of 4π sr.

The luminous intensity is given in candela or cd for short. Candela is the Latin word for candle, and in fact this unit was originally based on real candles: one candela should correspond approximately to the luminous intensity of a candle.

Candela is defined as the ratio of luminous flux and solid angle, i.e. lm/sr.

A real candle emits its light almost completely spherically. So if its luminous intensity is 1 cd, we can calculate its luminous flux: Luminous flux = luminous intensity × 4 × π = 12.57 lm.

Luminouse exitance

However, not every light source can be described as dot-like as a candle or a lamp from a distance of one meter or more. Due to their particular application, some light sources must be treated as a surface that radiates uniformly over its entire spread. For example, the surface of SMD LEDs is often viewed in this way, as a surface made up of lots of small point light sources whose beam angles overlap in such a way that the entire surface forms a uniformly radiating element.

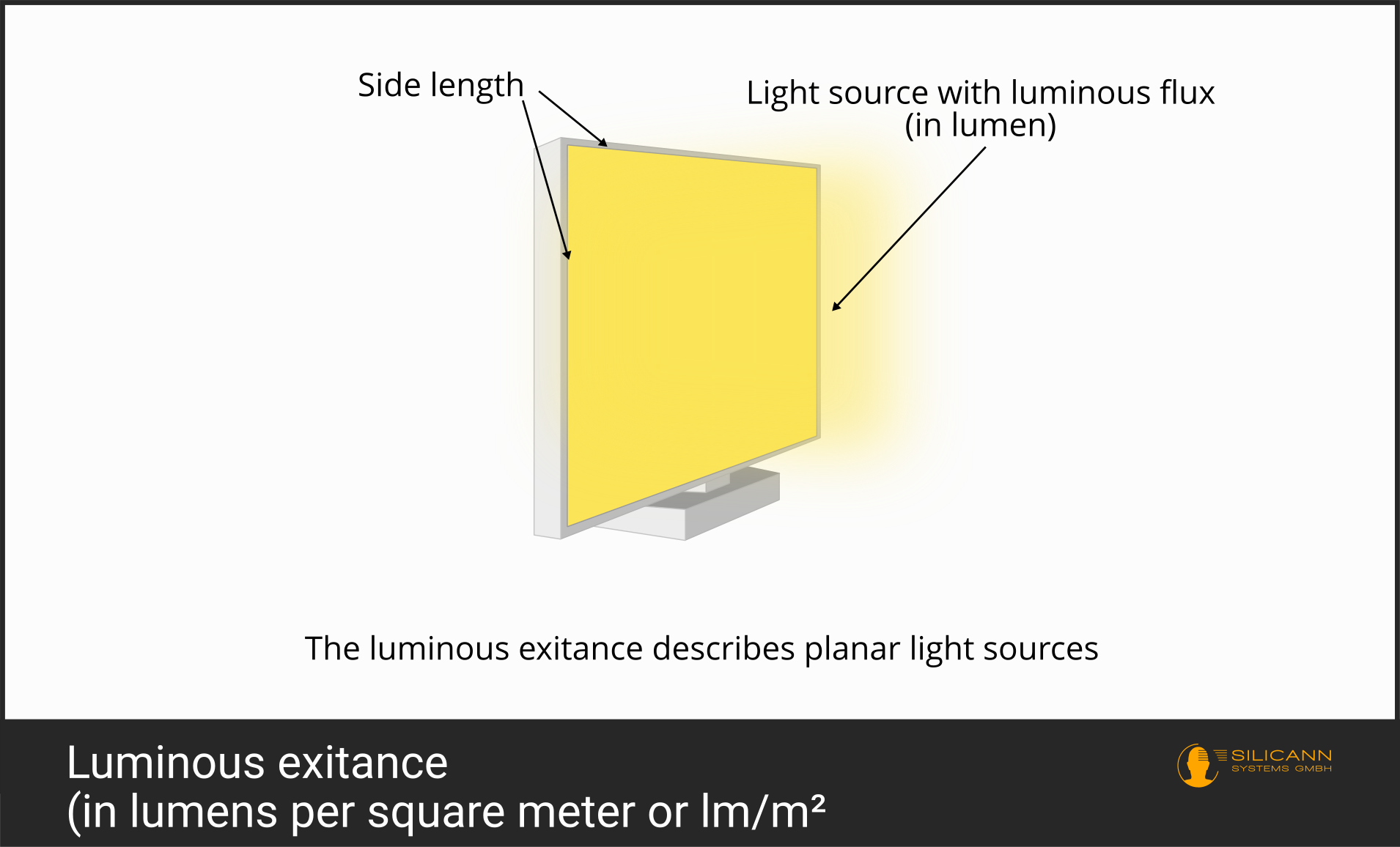
The luminous exitance of such plane radiators is then specified as lm/m²: The luminous flux it emits (stated in lumens) is in relation to the radiating surface (in m²).

Why is there this distinction between luminous flux and luminous exitance, i.e. why is the impression of brightness not simply expressed in lumens? Because our visual system classifies a light source as brighter if it emits the same luminous flux over a smaller area.

The emitting surface is therefore taken into account in the specific light output. However, the beam angle of the spotlight is not considered in this case.

Luminance

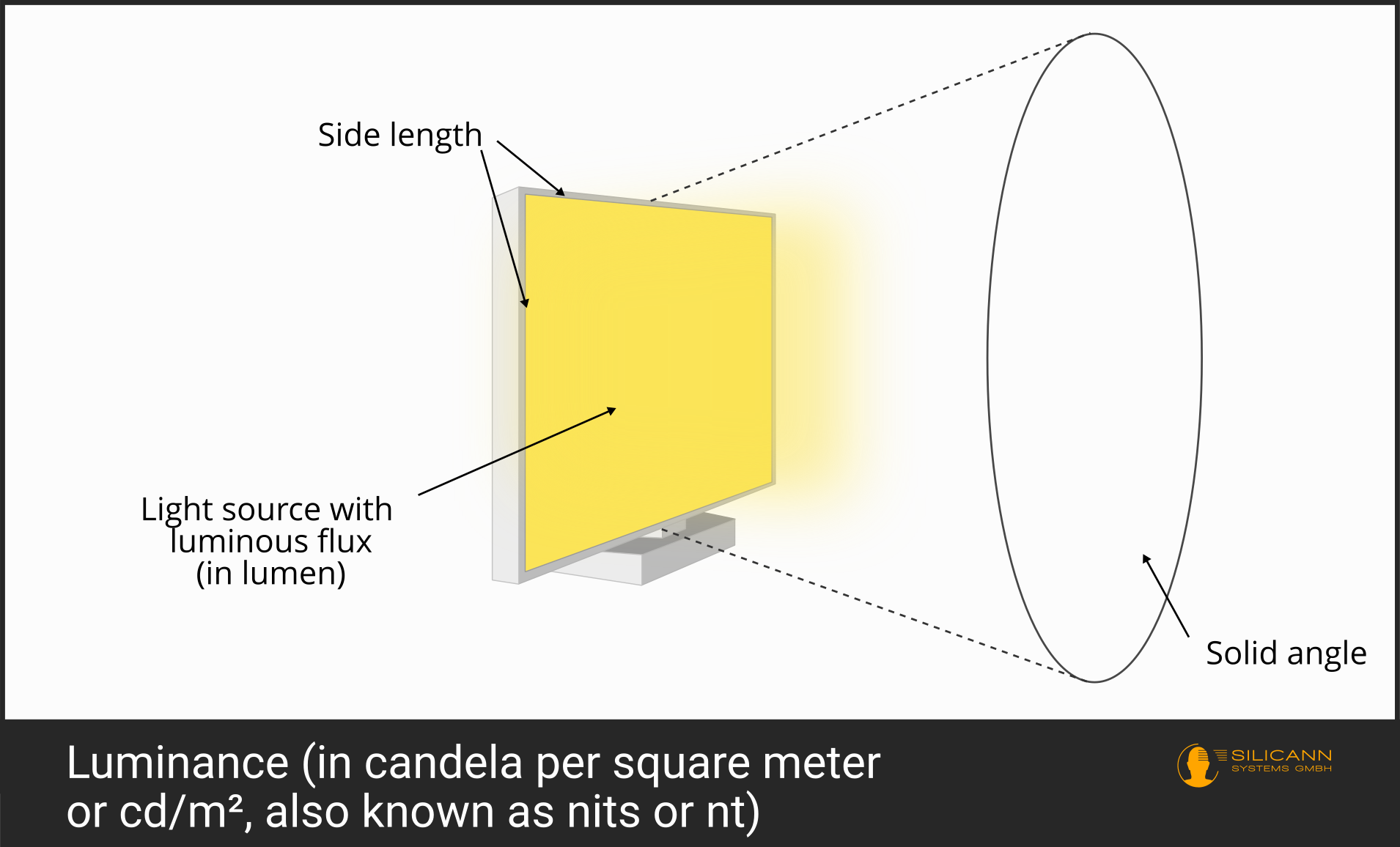
But you can't do this with every light source - in many cases the angle plays a major role in the impression of brightness that is created for the person looking at it. This applies, for example, to displays.

The luminance essentially describes a combination of the luminous exitance (i.e. the area of the emission) and simultaneous consideration of the solid angle within which the light is emitted.

We already know the solid angle from luminous intensity - there, however, the source of the light was simply assumed to be a point. So here we are basically dealing with the luminous intensity in relation to the radiating surface. Accordingly, the unit of luminance is candela per square meter.

Cd/m² is the SI unit for luminance and is used practically worldwide. Occasionally, however, the term nits is also used. It comes from the English-speaking world and means exactly the same thing: 1 nt = 1 cd/m².

Illuminance

All the physical quantities listed so far were used to describe light sources. However, there are also quantities that do not consider the source of light, but rather the illuminated surface.

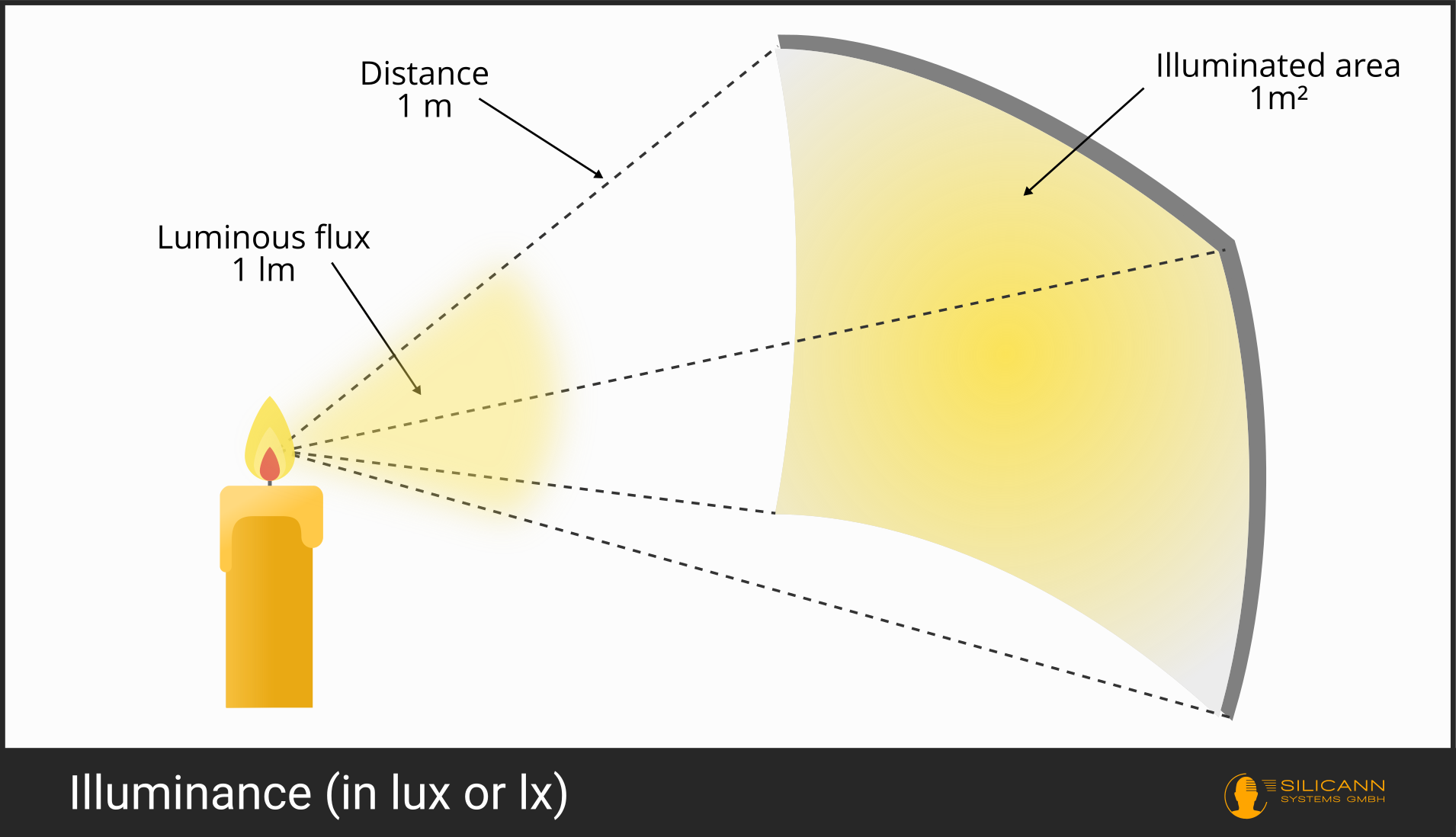
The ubiquitous quantity here is illuminance, probably better known by its unit lux.

Of course, illuminance does not deal with something fundamentally different, but merely shifts the frame of reference from the source of light to its target. This is why the unit lux is also derived from units that describe light sources. And it is again about illumination, not radiation, i.e. there is again the reference to the human visual system and the restriction to visible light instead of electromagnetic radiation in general.

The IEC has defined 1 lux as the illuminance produced by a luminous flux of 1 lumen on a (uniformly illuminated) surface of 1 square meter: lx = lm/m².

If we have the luminous intensity in candela instead of the luminous flux in lumen, we can also use this to calculate the illuminance. The luminous intensity extends the luminous flux by the solid angle of the radiation. If the light source is located at a distance of one meter and radiates over a solid angle of 1 sr, then it illuminates an area of exactly 1 m². 1 lux is therefore also equal to 1 candela per square meter - however, the meters here describe the distance between the light source and the illuminated surface, not the surface itself!

Converting the different photometric quantities.

Armed with the knowledge of the different photometric quantities, we can now also try to compare light sources and illuminated surfaces with each other, even if their properties have been specified in different quantities.

However, it is important that the conversion also makes physical sense - the existence of the appropriate units is not always sufficient here.

Converting luminous flux and luminous exitance

Converting between these two quantities is certainly the simplest scenario, because here we only need to know the area of the emitter. If we multiply the specific light emission by the area of the emitter, we obtain the luminous flux in lumens.

Calculating luminous flux and luminous intensity

If we have a point-shaped spotlight and a brightness specification in candela, then we only have to determine the solid angle of the radiation to obtain the luminous flux. If the light source emits light completely spherically, then its solid angle is 4 × π = 12.57 lumens per candela.

Or the other way round: a lamp with a brightness of 400 lm is equivalent to another light source with 31.8 cd:

400 lm / (4×π) = 31.8 cd.

Calculating luminous intensity and luminance

The main difference between luminous intensity and luminance is the size of the emitter: Luminous intensity assumes a point light source, while luminance is used to describe an area emitter.

There is a reason for this distinction, as described at the beginning, because our visual system perceives a light source with a smaller spatial spread as brighter than a light source of the same intensity but with a larger surface area.

However, if we want to compare a light source with luminous intensity in candelas and a light source with luminance in cd/m² in purely mathematical terms, then we simply have to multiply the latter by its surface area.

This would make little sense for the subjective impression of brightness (an LED with 300 candela would appear much brighter to us than a monitor with 300 cd/m²). However, we could calculate in this way if, for example, we want to answer the question of whether the LED and the monitor illuminate the same room to approximately the same extent.

Calculating luminous flux and luminance

The same concerns about the meaningfulness of a comparison also apply when comparing luminous flux and luminance. If the subjective impression of brightness can be ignored, then the value of the spotlight described by luminance must simply be multiplied by its area and 4 × π, the solid angle of a full sphere.

An example: We want to compare a 17" display with a brightness specification of 300 cd/m² and an incandescent lamp with 300 lm. A 17" display in 16:9 format has edge lengths of approx. 35.5 and 20 cm. Multiplied by the area (0.355 × 0.2) we get a luminous intensity of 21.3 cd. If we now multiply by 4 × π, we obtain a luminous flux of 267.7 lm. The incandescent lamp specified as 300 lm therefore emits slightly more light overall - but in all directions, when used without a lampshade.

Calculating with illuminance and luminous intensity

Illuminance is a little more interesting because, unlike all the other quantities described, it does not deal with the emitter but instead with the irradiated surface. On the other hand, the illuminated surface itself behaves as a radiator when we consider the light reflected from it.

In practice, light and lighting are often used in calculations when, for example, a certain illuminance is specified by standards and the appropriate light sources have to be determined on this basis.

For example, we would like to illuminate a workplace with 1000 lx. The lamp will hang at a distance of 80 cm above the table and its brightness is specified as luminous intensity, i.e. in candela. For the sake of simplicity, we assume that the light from the lamp exactly illuminates the surface of the table.

The mathematical relationship between the units is lux = candela per square meter. However, it is important to note that the square meters are not the illuminated area, but the square of the distance from the surface. The luminous intensity in candela describes the radiation in a certain solid angle, and this solid angle covers an area of one square meter at a distance of one meter.

In the case of our illuminated table, we must therefore multiply the illuminance by the square of the distance of the lamp:

1000 lx × 0.8 m² = 640 cd.

The lamp must therefore have a luminous intensity of at least 640 cd in order to illuminate the table with 1000 lx.

Converting illuminance and luminous flux

Let's stay with the example we just used, a work table is to be illuminated with 1000 lux. This time, however, we assume that the lamps are determined by their luminous flux, i.e. in the unit lumen.

Even if the lamp is specified in lumens, i.e. the beam angle is not taken into account by the manufacturer, we must also consider this solid angle in the real world. Let's assume that the lamp in this example, viewed from the side, has a beam angle of 90°.

In this case, we can use the relationship between luminous intensity and luminous flux: Luminous intensity is luminous flux divided by the solid angle of the beam.

So first we calculate the luminous intensity in candelas and then multiply by the solid angle to obtain the required luminous flux.

The specification is an illuminance of 1000 lux, and the lamp distance is still 80 cm. This means that the luminous intensity also remains the same: 640 cd.

Now we just need to calculate the solid angle. The problem is that we only have the specification of a plane angle, i.e. an angle in the surface, not in space.

From a plane angle to a solid angle

A solid angle does not have to describe a circular cone, but if it does, then it is relatively easy to convert between a solid angle and a plane angle.

First, let's look at the basic sense of the calculation. A solid angle can be described as a cone that has its origin at the center of a sphere and its base on the surface of the sphere. We can divide this sphere in half so that we are looking at the cross-section of the cone described by the solid angle. Because the surface, the base of the cone, is a circle, i.e. symmetrical, there is a clear relationship between this 2D cross-section and the three-dimensional cone.

The solid angle is calculated from the plane angle (in radians, not degrees) as follows:

spatial angle = 2×π×(1-cos(angle/2))

If the plane angle is in degrees instead of radians, then it works like this:

spatial angle = 2×π×(1-cos(angle×π/360))

Back to our illuminated work table: For a lamp with an opening angle of 90°, the solid angle of the emitted light has a value of 1.84 sr according to this formula. Luminous flux is equal to luminous intensity times solid angle. The luminous intensity was 640 cd, so we have the result: the lamp must have a luminous flux of 640 cd × 1.84 sr = 1177 lm.

Alternatively, the beam angle may be negligible, e.g. with an arrangement of LED panels on the ceiling. In this case, we can simply apply the formula lumen = lux × square meters. A suitable scenario: We want to achieve the same lighting in a room as outside on a cloudy winter's day, according to Wikipedia approx. 3500 lx. The fictitious room has a size of 30 m². Then we need panels on the ceiling with a luminous flux of a sporty 3500 × 30 = 105000 lm. Perhaps it can actually be a little darker in the room than outside.

Calculating illuminance and luminance

The resulting illuminance can also be derived from the luminance, usually used for displays - and vice versa. The scenario: A person is lying in bed in a dark room and using their cell phone. We want to calculate the illuminance on the surface of the face. It is already dark, so the display has been turned down to 200 cd/m². The display itself is 6.5 cm wide and 15 cm high and is held at a distance of 40 cm from the face.

First we have to multiply by the actual area of the display to get the luminous intensity in candela:

200 × (0.06 × 0.15)² = 1.95 candela.

We have now taken the area of the display out of the equation and only have the conversion from luminous intensity to illuminance that we have already discussed: illuminance = luminous intensity divided by distance²:

1.95 / 0.4² = 12.2 lux

Here, too, we can only ignore the angle of radiation because the angle of a cell phone display is just narrow enough for practically all the light to actually land on the face at the distance mentioned (the local field test showed a flat angle of approx. 10°, i.e. approx. 0.0024 sr). If a significant part of the light would miss the face or only irradiate a part of the face, then we would have to extend the calculation by the solid angle.